28.05.2021 Úmrtnostní tabulky za ČR, regiony soudržnosti a kraje - 2019–2020
Kód: 130063-21
|
Informační služby: tel: 274 052 304 E-mail: infoservis@czso.cz Kontakt: Ing. David Morávek E-mail: david.moravek@czso.cz |
Přílohy
| Všechna data publikace (2,3 MB) | ZIP |
| Metodické poznámky | Word PDF |
|
Podrobné úmrtnostní tabulky za ČR v roce 2020 |
|
| Česká republika, muži | Excel PDF |
| Česká republika, ženy | Excel PDF |
|
Podrobné úmrtnostní tabulky za regiony soudržnosti ČR v roce 2020 |
|
| Praha, muži | Excel PDF |
| Praha, ženy | Excel PDF |
| Střední Čechy, muži | Excel PDF |
| Střední Čechy, ženy | Excel PDF |
| Jihozápad, muži | Excel PDF |
| Jihozápad, ženy | Excel PDF |
| Severozápad, muži | Excel PDF |
| Severozápad, ženy | Excel PDF |
| Severovýchod, muži | Excel PDF |
| Severovýchod, ženy | Excel PDF |
| Jihovýchod, muži | Excel PDF |
| Jihovýchod, ženy | Excel PDF |
| Střední Morava, muži | Excel PDF |
| Střední Morava, ženy | Excel PDF |
| Moravskoslezsko, muži | Excel PDF |
| Moravskoslezsko, ženy | Excel PDF |
|
Podrobné úmrtnostní tabulky za kraje ČR v letech 2019–2020 |
|
| Hlavní město Praha, muži | Excel PDF |
| Hlavní město Praha, ženy | Excel PDF |
| Středočeský kraj, muži | Excel PDF |
| Středočeský kraj, ženy | Excel PDF |
| Jihočeský kraj, muži | Excel PDF |
| Jihočeský kraj, ženy | Excel PDF |
| Plzeňský kraj, muži | Excel PDF |
| Plzeňský kraj, ženy | Excel PDF |
| Karlovarský kraj, muži | Excel PDF |
| Karlovarský kraj, ženy | Excel PDF |
| Ústecký kraj, muži | Excel PDF |
| Ústecký kraj, ženy | Excel PDF |
| Liberecký kraj, muži | Excel PDF |
| Liberecký kraj, ženy | Excel PDF |
| Královéhradecký kraj, muži | Excel PDF |
| Královéhradecký kraj, ženy | Excel PDF |
| Pardubický kraj, muži | Excel PDF |
| Pardubický kraj, ženy | Excel PDF |
| Kraj Vysočina, muži | Excel PDF |
| Kraj Vysočina, ženy | Excel PDF |
| Jihomoravský kraj, muži | Excel PDF |
| Jihomoravský kraj, ženy | Excel PDF |
| Olomoucký kraj, muži | Excel PDF |
| Olomoucký kraj, ženy | Excel PDF |
| Zlínský kraj, muži | Excel PDF |
| Zlínský kraj, ženy | Excel PDF |
| Moravskoslezský kraj, muži | Excel PDF |
| Moravskoslezský kraj, ženy | Excel PDF |
|
Příloha |
|
| Naděje dožití ve vybraných věcích podle pohlaví v ČR, 2001–2020 | Excel PDF |
| Naděje dožití při narození podle pohlaví v regionech soudržnosti, 2001–2020 | Excel PDF |
| Naděje dožití při narození podle pohlaví v krajích, 2001–2020 | Excel PDF |
|
Kartogram |
|
| Naděje dožití mužů při narození v regionech soudržnosti v roce 2020 | PNG |
| Naděje dožití žen při narození v regionech soudržnosti v roce 2020 | PNG |
| Naděje dožití mužů při narození v krajích, 2019–2020 | PNG |
| Naděje dožití žen při narození v krajích, 2019–2020 | PNG |
|
Úmrtnostní tabulky za regiony soudržnosti ČR – retrospektivní roční údaje
(12,6 MB)
|
ZIP |
- rok 2021 | 2019–2020
- rok 2020 | 2018 - 2019
- rok 2019 | 2017 - 2018
- rok 2018 | 2016 - 2017
- rok 2017 | 2015 - 2016
- rok 2016 | 2014 - 2015
- rok 2015 | 2013 - 2014
- rok 2014 | 2012 až 2013
- rok 2013 | 2011 až 2012
- rok 2012 | 2010, 2011
- rok 2011 | 2010
- rok 2010 | 2008 - 2009
Zveřejněno dne: 28.05.2021
Data jsou platná ke dni zveřejnění publikace.
Základní metodické poznámky
Podrobné úmrtnostní tabulky za Českou republiku a její regiony soudržnosti a kraje jsou založeny na III. hlavních souborech demografických událostí. Vstupní pravděpodobnosti úmrtí jsou vypočteny nepřímou metodou, tj. odvozeny z pozorovaných specifických měr úmrtnosti (viz níže). Tabulky jsou podrobné, tj. s jednoletým věkovým intervalem, s nejvyšším věkovým intervalem 105 a více let. Jsou počítány odděleně pro muže a ženy.
S ohledem na vyloučení nahodilých výkyvů jsou tabulky pro kraje (NUTS 3) zpracovány za dvouleté kalendářní období. Od roku 2021 (počínaje obdobím 2020) jsou tabulky pro regiony soudržnosti zpracovány za jednoleté (dříve dvouleté) kalendářní období. Zejména z důvodu sledování dynamiky vývoje úmrtnosti ČSÚ připravil retrospektivní výpočet úmrtnostních tabulek zpracovaný jednotně v ročním pohledu od 2001. Územní členění odpovídá stavu platnému k 1. 1. každého daného roku.
Ukazatele úmrtnostních tabulek
Počet zemřelých (![]() )
uvádí absolutní počet zemřelých ve věku
)
uvádí absolutní počet zemřelých ve věku ![]() během
daného období.
během
daného období.
Počet obyvatel (![]() )
uvádí střední stav obyvatel ve věku
)
uvádí střední stav obyvatel ve věku ![]() .
V případě tabulek celostátních i tabulek za regiony soudržnosti a kraje je
střední stav definován jako bilancovaný počet obyvatel k 1. 7. daného
roku, resp. jako součet středních stavů v případě víceletých období.
.
V případě tabulek celostátních i tabulek za regiony soudržnosti a kraje je
střední stav definován jako bilancovaný počet obyvatel k 1. 7. daného
roku, resp. jako součet středních stavů v případě víceletých období.
Pravděpodobnost úmrtí (![]() )
vyjadřuje pravděpodobnost, že osoba dožívající se přesného věku
)
vyjadřuje pravděpodobnost, že osoba dožívající se přesného věku ![]() let
v daném období (tj. před dosažením věku
let
v daném období (tj. před dosažením věku ![]() )
zemře:
)
zemře:
![]() .
.
kde ![]() označuje
míru úmrtnosti v daném věku a parametr
označuje
míru úmrtnosti v daném věku a parametr ![]() vyčísluje
průměrný počet člověkoroků prožitých v daném věkovém intervalu zemřelými
jedinci (viz níže).
vyčísluje
průměrný počet člověkoroků prožitých v daném věkovém intervalu zemřelými
jedinci (viz níže).
Tabulkový počet dožívajících
(![]() )
je hypotetický počet osob, které se dožijí věku
)
je hypotetický počet osob, které se dožijí věku ![]() let
ze 100 000 živě narozených (kořen tabulky
let
ze 100 000 živě narozených (kořen tabulky ![]() )
při zachování řádu úmrtnosti sledovaného období:
)
při zachování řádu úmrtnosti sledovaného období:
![]() .
.
Tabulkový počet zemřelých (![]() )
vyjadřuje hypotetický počet zemřelých osob v dokončeném věku
)
vyjadřuje hypotetický počet zemřelých osob v dokončeném věku ![]() let;
je počítán jako rozdíl dvou po sobě jdoucích tabulkových počtů dožívajících:
let;
je počítán jako rozdíl dvou po sobě jdoucích tabulkových počtů dožívajících:
![]() .
.
Tabulkový počet žijících (![]() )
je hypotetický počet člověkoroků prožitých mezi přesnými věky
)
je hypotetický počet člověkoroků prožitých mezi přesnými věky ![]() a
a
![]() :
:
![]() .
.
Pomocný
ukazatel (![]() )
vyjadřuje počet let života, které má tabulková populace (nikoliv jednotlivec) v daném
věku
)
vyjadřuje počet let života, které má tabulková populace (nikoliv jednotlivec) v daném
věku ![]() ještě
před sebou, a je dán kumulací počtu žijících
ještě
před sebou, a je dán kumulací počtu žijících ![]() od
věku
od
věku ![]() do
nejvyššího věku tabulky:
do
nejvyššího věku tabulky:
![]() .
.
Střední délka života neboli
naděje dožití (![]() )
udává průměrný počet let, který prožije právě
)
udává průměrný počet let, který prožije právě ![]() -letá
osoba při zachování úmrtnostních poměrů daného období. Jedná se o souhrnný
ukazatel, který odráží úmrtnostní poměry ve všech věkových skupinách.
-letá
osoba při zachování úmrtnostních poměrů daného období. Jedná se o souhrnný
ukazatel, který odráží úmrtnostní poměry ve všech věkových skupinách.
![]() .
.
Podrobný postup konstrukce úmrtnostní tabulky
A. Zpracování vstupních dat
1. Výpočet pozorovaných měr úmrtnosti
Z
empirických dat je vypočtena tzv. reálná (pozorovaná)
míra úmrtnosti (![]() ),
jakožto podíl zemřelých a středního stavu obyvatel v daném věku, pohlaví a
územní jednotce:
),
jakožto podíl zemřelých a středního stavu obyvatel v daném věku, pohlaví a
územní jednotce:
![]() ,
,
![]() .
.
2. Vyrovnání pozorovaných měr úmrtnosti
Pro ošetření možných náhodných fluktuací reálných (pozorovaných) měr úmrtnosti, které jsou obzvláště běžné ve věcích s nízkou úmrtností nebo s nízkými počty žijících, jsou míry úmrtnosti vyhlazeny metodou zobecněných adaptivních modelů v kombinaci s tzv. P-spliny, někdy označováno jako metoda P-GAM (Eilers a Marx, 1996). Prediktorem je věk, predikovanou hodnotou počet zemřelých, počet obyvatel je použit jako offset. U počtů zemřelých se předpokládá Poissonovo rozdělení. Míra vyhlazení je „adaptována“ na počty zemřelých v daném věku, tzn. nižší počty zemřelých jsou vyhlazovány více než vysoké počty zemřelých, kde je tak zachována významnost původního jevu/trendu.
3. Modelování úmrtnosti ve vysokém věku
S ohledem
na nízké počty zemřelých ve vysokém věku a nižší spolehlivost údajů o středním
stavu nejstarší populace jsou vyrovnané pozorované míry úmrtnosti v nejvyšších
věcích nahrazeny modelovými hodnotami. Úmrtnostní modely přitom obecně pracují
se spojitou definicí míry úmrtnosti, tzv. force of mortality (někdy překládáno
jako síla úmrtnosti), značenou ![]() .
V praxi se předpokládá, že při monotónním nárůstu funkce úmrtnosti s věkem
přibližně platí následující vztah mezi sílou a mírou úmrtnosti v daném věku
(Thatcher a kol., 1998):
.
V praxi se předpokládá, že při monotónním nárůstu funkce úmrtnosti s věkem
přibližně platí následující vztah mezi sílou a mírou úmrtnosti v daném věku
(Thatcher a kol., 1998):
![]() .
.
Zde zvolený model je založen na logistické křivce, která zohledňuje zpomalení nárůstu úmrtnosti s věkem. Konkrétně jde o model, který poprvé použil Kannisto (Thatcher a kol., 1998). Výpočtový program tak modeluje věkově specifickou úmrtnost pomocí funkce:
![]() .
.
kde ![]() je
věk a
je
věk a ![]() ,
,
![]() jsou
jednotlivé parametry a
jsou
jednotlivé parametry a ![]() je
konstanta. Parametry funkce jsou odhadnuty metodou maximální věrohodnosti.
Výchozí odhad parametrů je založen na předpokladu Poissonova rozdělení počtů
zemřelých (
je
konstanta. Parametry funkce jsou odhadnuty metodou maximální věrohodnosti.
Výchozí odhad parametrů je založen na předpokladu Poissonova rozdělení počtů
zemřelých (![]() )
ve věku
)
ve věku ![]() .
Na základě těchto předpokladů je pak maximalizován logaritmus věrohodnostní
funkce (
.
Na základě těchto předpokladů je pak maximalizován logaritmus věrohodnostní
funkce (![]() )
ve tvaru:
)
ve tvaru:
![]()
![]() .
.
Při optimalizaci (záporného logaritmu) věrohodnostní funkce program pracuje s vlastními počátečními hodnotami parametrů. Pro odhad parametrů je nastaveno věkové rozpětí 70–90 let.
Při
přechodu z vyrovnaných na modelové hodnoty se předpokládá, že věk, od kterého
modelové hodnoty charakterizují úmrtnost lépe než vyrovnané hodnoty, je vyšší
než 75 let. Pro hladký průběh nahrazení vyrovnaných hodnot modelovými hodnotami
se nejprve hledá věk ![]() vyšší
než 75 let, kde je pozorován nejnižší rozdíl mezi vyrovnanou a modelovou mírou
úmrtnosti, tzn. takový věk
vyšší
než 75 let, kde je pozorován nejnižší rozdíl mezi vyrovnanou a modelovou mírou
úmrtnosti, tzn. takový věk ![]() ,
pro který platí:
,
pro který platí:
![]() , y ? 75 .
, y ? 75 .
Po
nalezení věku ![]() pak
provedeme postupnou graduaci vyrovnaných na modelové hodnoty pro věky
pak
provedeme postupnou graduaci vyrovnaných na modelové hodnoty pro věky
![]() dle
vztahu:
dle
vztahu:
![]() .
.
4. Pro výpočet úmrtnostní tabulky je použita následující kombinace hodnot věkově specifických měr úmrtnosti:
pro věk 0: reálné (pozorované) hodnoty,
pro
věk 1 až ![]() : vyrovnané
hodnoty,
: vyrovnané
hodnoty,
pro
věk ![]() až
až
![]() : graduace
mezi vyrovnanými a modelovými hodnotami,
: graduace
mezi vyrovnanými a modelovými hodnotami,
pro
věk ![]() a
vyšší: modelové hodnoty.
a
vyšší: modelové hodnoty.
B. Převod reálných vyrovnaných dat na tabulkové
Základem pro výpočet úmrtnostní
tabulky nepřímou metodou je převod věkově specifických měr úmrtnosti (![]() )
na pravděpodobnosti úmrtí (
)
na pravděpodobnosti úmrtí (![]() ).
Za předpokladu rovnosti reálné a tabulkové míry úmrtnosti a za předpokladu
stability měr úmrtnosti v hypotetické tabulkové kohortě používáme následující
převodní rovnici (Chiang, 1984):
).
Za předpokladu rovnosti reálné a tabulkové míry úmrtnosti a za předpokladu
stability měr úmrtnosti v hypotetické tabulkové kohortě používáme následující
převodní rovnici (Chiang, 1984):
![]() .
.
Parametr ![]() vyčísluje
průměrný počet člověkoroků prožitých v daném věkovém intervalu zemřelými
jedinci. Hodnotu
vyčísluje
průměrný počet člověkoroků prožitých v daném věkovém intervalu zemřelými
jedinci. Hodnotu ![]() lze
pozorovat přímo z reálných dat (jsou-li k dispozici přesné věky zemřelých tak
jako jejich průměr), alternativně ji lze odvodit z pozorovaných úmrtnostních
měr nebo převzít z populace s podobným řádem vymírání (Preston a kol., 2000). S
ohledem na obecně platný předpoklad rovnoměrného rozložení přesného věku
zemřelých je použita hodnota 0,5 pro všechny věky s výjimkou věku 0 a
posledního (otevřeného) věkového intervalu. V případě odhadu průměrného
věku zemřelých kojenců (
lze
pozorovat přímo z reálných dat (jsou-li k dispozici přesné věky zemřelých tak
jako jejich průměr), alternativně ji lze odvodit z pozorovaných úmrtnostních
měr nebo převzít z populace s podobným řádem vymírání (Preston a kol., 2000). S
ohledem na obecně platný předpoklad rovnoměrného rozložení přesného věku
zemřelých je použita hodnota 0,5 pro všechny věky s výjimkou věku 0 a
posledního (otevřeného) věkového intervalu. V případě odhadu průměrného
věku zemřelých kojenců (![]() )
je využit nejpřesnější způsob výpočtu přímo z pozorovaných dat (Andreev a
Kingkade, 2015), kdy je hodnota
)
je využit nejpřesnější způsob výpočtu přímo z pozorovaných dat (Andreev a
Kingkade, 2015), kdy je hodnota ![]() vypočtena
z reálných individuálních dat jakožto pozorovaný podíl průměrného věku
zemřelých kojenců (ve dnech) na celkovém trvání kalendářního roku (365 dní):
vypočtena
z reálných individuálních dat jakožto pozorovaný podíl průměrného věku
zemřelých kojenců (ve dnech) na celkovém trvání kalendářního roku (365 dní):
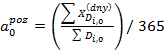 .
.
kde ![]() je
individuální úmrtí v kojeneckém věku a
je
individuální úmrtí v kojeneckém věku a ![]() individuální
věk zemřelého kojence ve dnech. Hodnota
individuální
věk zemřelého kojence ve dnech. Hodnota ![]() je
nastavena jako jeden z parametrů (výchozí defaultní hodnota je 0,1).
V případě nižších územních celků se vždy uvádí hodnota vypočtená
z dat za celou ČR v daném období.
je
nastavena jako jeden z parametrů (výchozí defaultní hodnota je 0,1).
V případě nižších územních celků se vždy uvádí hodnota vypočtená
z dat za celou ČR v daném období.
U poslední otevřené věkové
skupiny (zde 105+) je parametr ![]() vypočten
jako (viz např. Preston a kol., 2000):
vypočten
jako (viz např. Preston a kol., 2000):
![]() .
.
Další postup výpočtu úmrtnostních tabulek navazuje na
vypočtené hodnoty ![]() (viz
Ukazatele úmrtnostních tabulek).
(viz
Ukazatele úmrtnostních tabulek).
Použitá literatura
Andreev, E. a Kingkade, W. W. (2015). Average age at death in infancy and infant mortality level: Reconsidering the Coale-Demeny formulas at current levels of low mortality. Demographic Research. 33(13): 363-390.
Eilers, P. H. C. a Marx B. D. (1996). Flexible Smoothing with B-splines and Penalties. Statistical Science. 11(2):89–121.
Chiang, C. L. (1984). The Life Table and Its Applications. Robert E. Krieger Publishing Company, Malabar, FL, USA.
Preston, S. H., Heuveline, P., Guillot, M. (2001). Demography: Measuring and modeling population processes. Oxford: Blackwell Publishers.
Thatcher, A., Kannisto, V., a Vaupel, J. W. (1998). The Force of Mortality at Ages 80 to 120. Odense, Denmark: Odense University Press.
Poslední zprávy z rubriky Z regionů:
Přečtěte si také:
Obrázky na stránce
Příbuzné stránky
- Platové tabulky - základní platová tabulka 2020
- Výpočet čisté mzdy v roce 2021 i v předchozích letech, změny v roce 2021
- Příspěvek na bydlení v roce 2021 - Kalkulačka
- Kalkulačka online 2021 i 2020 - čistá mzda, hypotéky a další kalkulačky
- Minimální mzda v roce 2021, 2020 i v minulosti, vliv na zaručenou mzdu
- Minimální mzda v roce 2021, 2020 i v minulosti, vliv na zaručenou mzdu
- Prázdniny 2020/2021
- Velikonoce 2021 od 21. 3. do 12. 4.
- Jarní prázdniny 2021
- Důchod a penze 2021 - aktuální informace k důchodům
- Velikonoční prázdniny 2021
- Zaručená mzda 2021 a 2020
Prezentace
02.04.2025 Firmy a podnikatelé si loni půjčili 168…
14.03.2025 MacBook za polovinu. V Česku je nová služba,…
10.03.2025 Nejpopulárnější Samsung má nástupce.










